NOLA NEURTU ITZALA ERABILIZ.

Eraikin erraldoiak edo naturaren garaiera handiak neurtzeak beti eragin ditu buruhausteak. Hala gertatu zen Egipton Keops piramidearekin. Norbaitek problema hori ebatziz gero, jakintsu ospea lortzen zuen. Horixe gertatu zitzaion Mileto-ko Tales jakintsuari, K.a. VI. mendean faraoiak Keops piramidearen altuera neurtzeko ardura eman zionean.
Zeregin horretarako, tramankulu konplexuz inguratuta azaltzea espero zuten denek. Baina agertu zenean, Talesek makila bat besterik ez zeraman. Egipton maiz gertatzen den bezala, egun eguzkitsu zoragarria zen. Talesek makila lurrarekiko perpendikular sartu zuen, eta makilaren itzala eta makila bera berdinak izan arte zain egon zen. Hori gertatu bezain pronto “Neur ezazue piramidearen itzala" agindu zien faraoiaren langileei. “Une honetan piramidearen altuera itzalaren luzera bezalakoa da".
Langileek piramidearen itzala neurtu zuten, eta neurri horri haren oinarriaren erdia gehitu zioten, itzalaren zati bat jaten zuelako. Horrela, eraikin handientsu haren altuera jakin zuten.
Prozedurak beste abantaila bat zeukan, erraza eta praktikoa izateaz gain: matematikariek egiaztatu zuten berdin zela bi objekturen itzalak berdinak izan edo ez. Makilaren itzala haren erdia bada, neurtu nahi dugun objektuaren itzala ere erdia izango da. Itzala herena bada, objektuaren itzalarekin berdin gertatuko da.
Talesen burutazio bikain hura teoria garrantzitsu batean oinarritzen zen: Triangeluen antzekotasuna
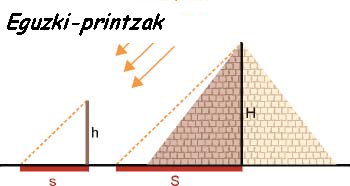
Triangelu txikia handitik atera dugula esan liteke. Handiarekiko forma berbera mantentzen du, baina tamaina txikiagotu egin da. Triangelu mota horietan alde baliokideen arteko proportzioa beti da berdina.
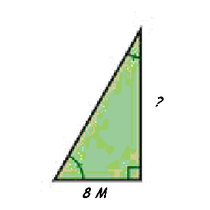
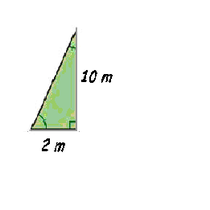
Demagun triangelu txikiaren altuera eta oinarriaren neurriak 10 eta 2 direla, hurrenez hurren; triangelu handiaren oinarria 8 bada, erraz kalkula dezakegu altuera 40 dela (txikiaren altuera halako lau izan behar delako).
40 da, hain zuzen, triangeluak proportzional bihurtzen dituena.

THATQUIZ. Geogebra: triangeluak
 Matematika 3.zikloa
Matematika 3.zikloa